Option Pricing via Machine Learning

Note

You are reading Tidy Finance with Python. You can find the equivalent chapter for the sibling Tidy Finance with R here.

This chapter covers machine learning methods in option pricing. First, we briefly introduce regression trees, random forests, and neural networks; these methods are advocated as highly flexible universal approximators, capable of recovering highly non-linear structures in the data. As the focus is on implementation, we leave a thorough treatment of the statistical underpinnings to other textbooks from authors with a real comparative advantage on these issues. We show how to implement random forests and deep neural networks with tidy principles using scikit-learn.

Machine learning (ML) is seen as a part of artificial intelligence. ML algorithms build a model based on training data in order to make predictions or decisions without being explicitly programmed to do so. While ML can be specified along a vast array of different branches, this chapter focuses on so-called supervised learning for regressions. The basic idea of supervised learning algorithms is to build a mathematical model for data that contains both the inputs and the desired outputs. In this chapter, we apply well-known methods such as random forests and neural networks to a simple application in option pricing. More specifically, we create an artificial dataset of option prices for different values based on the Black-Scholes pricing equation for call options. Then, we train different models to learn how to price call options without prior knowledge of the theoretical underpinnings of the famous option pricing equation by Black and Scholes (1973).

Throughout this chapter, we need the following Python packages.

import pandas as pd 
import numpy as np

from plotnine import *
from itertools import product
from scipy.stats import norm
from sklearn.model_selection import train_test_split
from sklearn.pipeline import Pipeline
from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import StandardScaler
from sklearn.ensemble import RandomForestRegressor
from sklearn.neural_network import MLPRegressor
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import Lasso

Regression Trees and Random Forests

Regression trees are a popular ML approach for incorporating multiway predictor interactions. In Finance, regression trees are gaining popularity, also in the context of asset pricing (see, e.g., Bryzgalova, Pelger, and Zhu 2022). Trees possess a logic that departs markedly from traditional regressions. Trees are designed to find groups of observations that behave similarly to each other. A tree grows in a sequence of steps. At each step, a new branch sorts the data leftover from the preceding step into bins based on one of the predictor variables. This sequential branching slices the space of predictors into partitions and approximates the unknown function \(f(x)\) which yields the relation between the predictors \(x\) and the outcome variable \(y\) with the average value of the outcome variable within each partition. For a more thorough treatment of regression trees, we refer to Coqueret and Guida (2020).

Formally, we partition the predictor space into \(J\) non-overlapping regions, \(R_1, R_2, \ldots, R_J\). For any predictor \(x\) that falls within region \(R_j\), we estimate \(f(x)\) with the average of the training observations, \(\hat y_i\), for which the associated predictor \(x_i\) is also in \(R_j\). Once we select a partition \(x\) to split in order to create the new partitions, we find a predictor \(j\) and value \(s\) that define two new partitions, called \(R_1(j,s)\) and \(R_2(j,s)\), which split our observations in the current partition by asking if \(x_j\) is bigger than \(s\): \[R_1(j,s) = \{x \mid x_j < s\} \mbox{ and } R_2(j,s) = \{x \mid x_j \geq s\}. \tag{1}\] To pick \(j\) and \(s\), we find the pair that minimizes the residual sum of square (RSS): \[\sum_{i:\, x_i \in R_1(j,s)} (y_i - \hat{y}_{R_1})^2 + \sum_{i:\, x_i \in R_2(j,s)} (y_i - \hat{y}_{R_2})^2 \tag{2}\] As in Factor Selection via Machine Learning in the context of penalized regressions, the first relevant question is: What are the hyperparameter decisions? Instead of a regularization parameter, trees are fully determined by the number of branches used to generate a partition (sometimes one specifies the minimum number of observations in each final branch instead of the maximum number of branches).

Models with a single tree may suffer from high predictive variance. Random forests address these shortcomings of decision trees. The goal is to improve the predictive performance and reduce instability by averaging multiple regression trees. A forest basically implies creating many regression trees and averaging their predictions. To assure that the individual trees are not the same, we use a bootstrap to induce randomness. More specifically, we build \(B\) decision trees \(T_1, \ldots, T_B\) using the training sample. For that purpose, we randomly select features to be included in the building of each tree. For each observation in the test set, we then form a prediction \(\hat{y} = \frac{1}{B}\sum\limits_{i=1}^B\hat{y}_{T_i}\).

Neural Networks

Roughly speaking, neural networks propagate information from an input layer, through one or multiple hidden layers, to an output layer. While the number of units (neurons) in the input layer is equal to the dimension of the predictors, the output layer usually consists of one neuron (for regression) or multiple neurons for classification. The output layer predicts the future data, similar to the fitted value in a regression analysis. Neural networks have theoretical underpinnings as universal approximators for any smooth predictive association (Hornik 1991). Their complexity, however, ranks neural networks among the least transparent, least interpretable, and most highly parameterized ML tools. In finance, applications of neural networks can be found in many different contexts, e.g., Avramov, Cheng, and Metzker (2022), Chen, Pelger, and Zhu (2023), and Gu, Kelly, and Xiu (2020).

Each neuron applies a non-linear activation function \(f\) to its aggregated signal before sending its output to the next layer \[x_k^l = f\left(\theta^k_{0} + \sum\limits_{j = 1}^{N ^l}z_j\theta_{l,j}^k\right) \tag{3}\] Here, \(\theta\) are the parameters to fit, \(N^l\) denotes the number of units (a hyperparameter to tune), and \(z_j\) are the input variables which can be either the raw data or, in the case of multiple chained layers, the outcome from a previous layer \(z_j = x_k-1\). While the easiest case with \(f(x) = \alpha + \beta x\) resembles linear regression, typical activation functions are sigmoid (i.e., \(f(x) = (1+e^{-x})^{-1}\)) or ReLu (i.e., \(f(x) = max(x, 0)\)).

Neural networks gain their flexibility from chaining multiple layers together. Naturally, this imposes many degrees of freedom on the network architecture for which no clear theoretical guidance exists. The specification of a neural network requires, at a minimum, a stance on depth (number of hidden layers), the activation function, the number of neurons, the connection structure of the units (dense or sparse), and the application of regularization techniques to avoid overfitting. Finally, learning means to choose optimal parameters relying on numerical optimization, which often requires specifying an appropriate learning rate. Despite these computational challenges, implementation in Python is not tedious at all because we can use the API to TensorFlow.

Option Pricing

To apply ML methods in a relevant field of finance, we focus on option pricing. The application in its core is taken from Hull (2020). In its most basic form, call options give the owner the right but not the obligation to buy a specific stock (the underlying) at a specific price (the strike price \(K\)) at a specific date (the exercise date \(T\)). The Black-Scholes price (Black and Scholes 1973) of a call option for a non-dividend-paying underlying stock is given by \[ \begin{aligned} C(S, T) &= \Phi(d_1)S - \Phi(d_2)Ke^{-r T} \\ d_1 &= \frac{1}{\sigma\sqrt{T}}\left(\ln\left(\frac{S}{K}\right) + \left(r_f + \frac{\sigma^2}{2}\right)T\right) \\ d_2 &= d_1 - \sigma\sqrt{T} \end{aligned} \tag{4}\] where \(C(S, T)\) is the price of the option as a function of today’s stock price of the underlying, \(S\), with time to maturity \(T\), \(r_f\) is the risk-free interest rate, and \(\sigma\) is the volatility of the underlying stock return. \(\Phi\) is the cumulative distribution function of a standard normal random variable.

The Black-Scholes equation provides a way to compute the arbitrage-free price of a call option once the parameters \(S, K, r_f, T\), and \(\sigma\) are specified (arguably, in a realistic context, all parameters are easy to specify except for \(\sigma\) which has to be estimated). A simple R function allows computing the price as we do below.

def black_scholes_price(S, K, r, T, sigma):
    """Calculate Black Scholes option price."""
  
    d1 = (np.log(S/K)+(r+sigma**2/2)*T)/(sigma*np.sqrt(T))
    d2 = d1-sigma*np.sqrt(T)
    price = S*norm.cdf(d1)-K*np.exp(-r*T)*norm.cdf(d2)
    
    return price

Learning Black-Scholes

We illustrate the concept of ML by showing how ML methods learn the Black-Scholes equation after observing some different specifications and corresponding prices without us revealing the exact pricing equation.

Data simulation

To that end, we start with simulated data. We compute option prices for call options for a grid of different combinations of times to maturity (T), risk-free rates (r), volatilities (sigma), strike prices (K), and current stock prices (S). In the code below, we add an idiosyncratic error term to each observation such that the prices considered do not exactly reflect the values implied by the Black-Scholes equation.

In order to keep the analysis reproducible, we use np.random.seed(). A random seed specifies the start point when a computer generates a random number sequence and ensures that our simulated data is the same across different machines.

random_state = 42
np.random.seed(random_state)

S = np.arange(40, 61)
K = np.arange(20, 91)
r = np.arange(0, 0.051, 0.01)
T = np.arange(3/12, 2.01, 1/12)
sigma = np.arange(0.1, 0.81, 0.1)

option_prices = pd.DataFrame(
  product(S, K, r, T, sigma),
  columns=["S", "K", "r", "T", "sigma"]
)

option_prices["black_scholes"] = black_scholes_price(
  option_prices["S"].values, 
  option_prices["K"].values, 
  option_prices["r"].values, 
  option_prices["T"].values, 
  option_prices["sigma"].values
)

option_prices = (option_prices
  .assign(
    observed_price=lambda x: (
      x["black_scholes"] + np.random.normal(scale=0.15)
    )
  )
)

The code above generates more than 1.5 million random parameter constellations (in the definition of the option_prices dataframe). For each of these values, the true prices reflecting the Black-Scholes model are given and a random innovation term pollutes the observed prices. The intuition of this application is simple: the simulated data provides many observations of option prices, by using the Black-Scholes equation we can evaluate the actual predictive performance of a ML method, which would be hard in a realistic context where the actual arbitrage-free price would be unknown.

Next, we split the data into a training set (which contains 1 percent of all the observed option prices) and a test set that will only be used for the final evaluation. Note that the entire grid of possible combinations contains python len(option_prices.columns) different specifications. Thus, the sample to learn the Black-Scholes price contains only 31,489 observations and is therefore relatively small.

train_data, test_data = train_test_split(
  option_prices, 
  test_size=0.01, random_state=random_state
)

We process the training dataset further before we fit the different ML models. We define a ColumnTransformer() that defines all processing steps for that purpose. For our specific case, we want to explain the observed price by the five variables that enter the Black-Scholes equation. The true price (stored in column black_scholes) should obviously not be used to fit the model. The recipe also reflects that we standardize all predictors via StandardScaler() to ensure that each variable exhibits a sample average of zero and a sample standard deviation of one.

preprocessor = ColumnTransformer(
  transformers=[(
    "normalize_predictors", 
     StandardScaler(),
     ["S", "K", "r", "T", "sigma"]
  )],
  remainder="drop"
)

Single layer networks and random forests

Next, we show how to fit a neural network to the data. The function MLPRegressor() from the package scikit-learn provides the functionality to initialize a single layer, feed-forward neural network. The specification below defines a single layer feed-forward neural network with ten hidden units. We set the number of training iterations to max_iter=1000.

max_iter = 1000

nnet_model = MLPRegressor(
  hidden_layer_sizes=10, 
  max_iter=max_iter, 
  random_state=random_state
)

We can follow the straightforward workflow as in the chapter before: define a workflow, equip it with the recipe, and specify the associated model. Finally, fit the model with the training data.

nnet_pipeline = Pipeline([
  ("preprocessor", preprocessor),
  ("regressor", nnet_model)
])

nnet_fit = nnet_pipeline.fit(
  train_data.drop(columns=["observed_price"]), 
  train_data.get("observed_price")
)

One word of caution regarding the training of Neural networks: For illustrative purposes we sequentially update the parameters by reiterating through the data 1,000 times (max_iter=1000). Typically, however, early stopping rules are advised that aim to interrupt the process of updating parameters as soon as the predictive performance on the validation test seems to deteriorate. A detailed discussion of these details in the implementation would go beyond the scope of this book.

Once you are familiar with the scikit-learn workflow, it is a piece of cake to fit other models. For instance, the model below initializes a random forest with 50 trees contained in the ensemble, where we require at least 2000 observations in a node. The random forests are trained using the function RandomForestRegressor().

rf_model = RandomForestRegressor(
  n_estimators=50, 
  min_samples_leaf=2000, 
  random_state=random_state
)

Fitting the model follows exactly the same convention as for the neural network before.

rf_pipeline = Pipeline([
  ("preprocessor", preprocessor),
  ("regressor", rf_model)
])

rf_fit = rf_pipeline.fit(
  train_data.drop(columns=["observed_price"]), 
  train_data.get("observed_price")
)

Deep neural networks

A deep neural network is a neural network with multiple layers between the input and output layers. By chaining multiple layers together, more complex structures can be represented with fewer parameters than simple shallow (one-layer) networks as the one implemented above. For instance, image or text recognition are typical tasks where deep neural networks are used (for applications of deep neural networks in finance, see, for instance, Jiang, Kelly, and Xiu 2023; Jensen et al. 2022). The following code chunk implements a deep neural network with three hidden layers of size ten each and logistic activation functions.

deepnnet_model = MLPRegressor(
  hidden_layer_sizes=(10, 10, 10),
  activation="logistic", 
  solver="lbfgs",
  max_iter=max_iter, 
  random_state=random_state
)
                              
deepnnet_pipeline = Pipeline([
  ("preprocessor", preprocessor),
  ("regressor", deepnnet_model)
])

deepnnet_fit = deepnnet_pipeline.fit(
  train_data.drop(columns=["observed_price"]),
  train_data.get("observed_price")
)

Universal approximation

Before we evaluate the results, we implement one more model. In principle, any non-linear function can also be approximated by a linear model containing the input variables’ polynomial expansions. To illustrate this, we include polynomials up to the fifth degree of each predictor and then add all possible pairwise interaction terms. We fit a Lasso regression model with a pre-specified penalty term (consult Factor Selection via Machine Learning on how to tune the model hyperparameters).

lm_pipeline = Pipeline([
  ("polynomial", PolynomialFeatures(degree=5, 
                                    interaction_only=False, 
                                    include_bias=True)),
  ("scaler", StandardScaler()),
  ("regressor", Lasso(alpha=0.01))
])

lm_fit = lm_pipeline.fit(
  train_data.get(["S", "K", "r", "T", "sigma"]),
  train_data.get("observed_price")
)

Prediction Evaluation

Finally, we collect all predictions to compare the out-of-sample prediction error evaluated on 10,000 new data points.

test_X = test_data.get(["S", "K", "r", "T", "sigma"])
test_y = test_data.get("observed_price")

predictive_performance = (pd.concat(
    [test_data.reset_index(drop=True), 
     pd.DataFrame({"Random forest": rf_fit.predict(test_X),
                   "Single layer": nnet_fit.predict(test_X),
                   "Deep NN": deepnnet_fit.predict(test_X),
                   "Lasso": lm_fit.predict(test_X)})
    ], axis=1)
  .melt(
    id_vars=["S", "K", "r", "T", "sigma",
             "black_scholes", "observed_price"],
    var_name="Model",
    value_name="Predicted"
  )
  .assign(
    moneyness=lambda x: x["S"]-x["K"],
    pricing_error=lambda x: np.abs(x["Predicted"]-x["black_scholes"])
  )
)

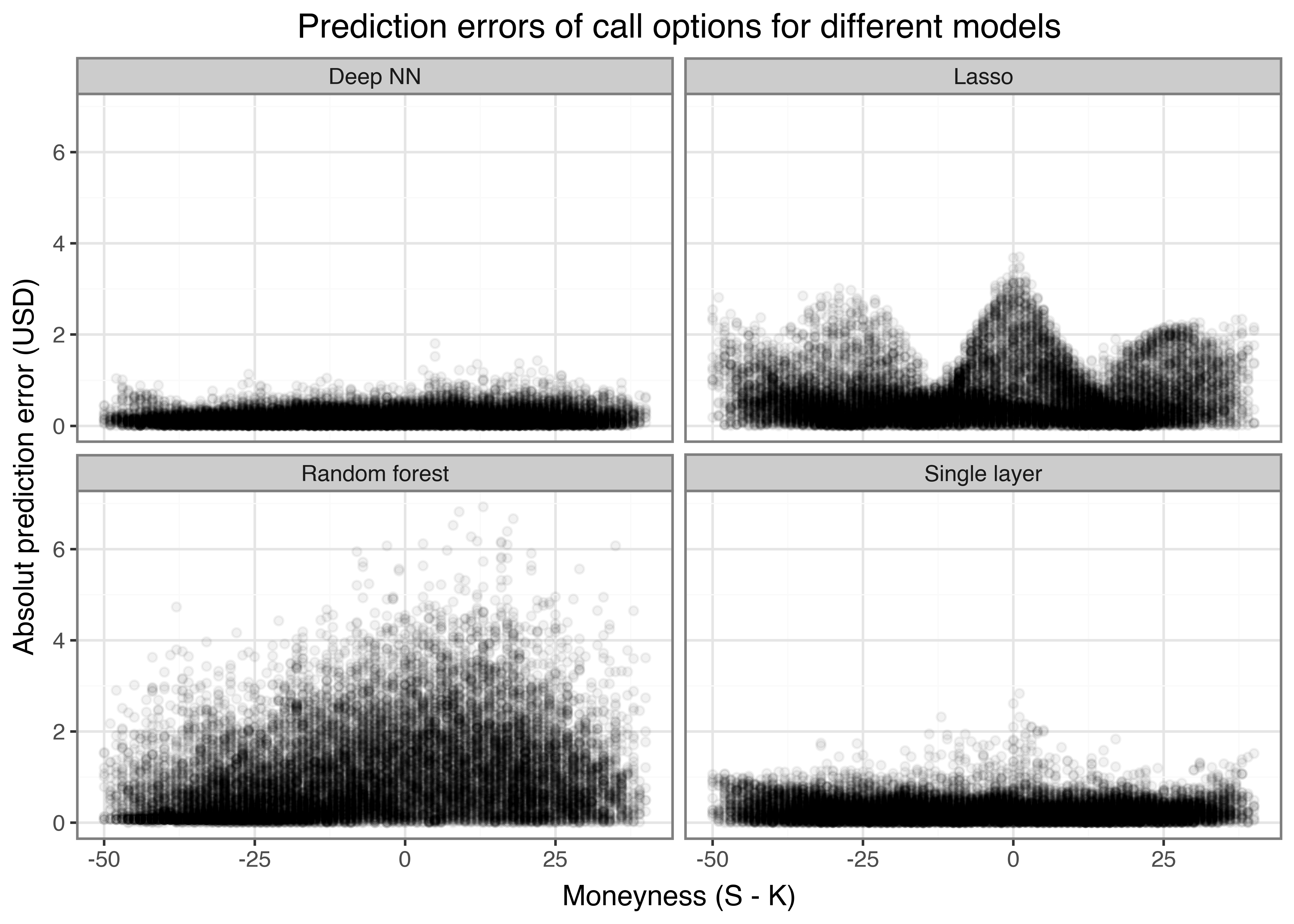
In the lines above, we use each of the fitted models to generate predictions for the entire test dataset of option prices. We evaluate the absolute pricing error as one possible measure of pricing accuracy, defined as the absolute value of the difference between predicted option price and the theoretical correct option price from the Black-Scholes model. We show the results graphically in Figure 1.

predictive_performance_plot = (
  ggplot(predictive_performance, 
         aes(x="moneyness", y="pricing_error")) +
  geom_point(alpha=0.05) +
  facet_wrap("Model") + 
  labs(x="Moneyness (S - K)", y="Absolut prediction error (USD)",
       title="Prediction errors of call options for different models") +
  theme(legend_position="")
)
predictive_performance_plot.draw()

Title: Prediction errors of call option prices for different models. The figure shows the pricing error of the different machine learning methods for call options for different levels of moneyness (strike price minus stock price). The figure indicates variation across the models and across moneyness. The random forest approach performs worst, in particular out of the money. — Figure 1: The figure shows absolut prediction error in USD for the different fitted methods. The prediction error is evaluated on a sample of call options that were not used for training.

The results can be summarized as follows:

All ML methods seem to be able to price call options after observing the training test set.
Random forest and the Lasso seem to perform consistently worse in predicting option prices than the neural networks.
For random forest and Lasso, the average prediction errors increase for far in-the-money options.
The increased complexity of the deep neural network relative to the single-layer neural network results in lower prediction errors.

Exercises

Write a function that takes y and a matrix of predictors X as inputs and returns a characterization of the relevant parameters of a regression tree with one branch.
Create a function that creates predictions for a new matrix of predictors newX based on the estimated regression tree.

References

Avramov, Doron, Si Cheng, and Lior Metzker. 2022. “Machine learning vs. economic restrictions: Evidence from stock return predictability.” Management Science 69 (5): 2547–3155. http://dx.doi.org/10.2139/ssrn.3450322.

Black, Fischer, and Myron Scholes. 1973. “The pricing of options and corporate liabilities.” Journal of Political Economy 81 (3): 637–54. https://www.jstor.org/stable/1831029.

Bryzgalova, Svetlana, Markus Pelger, and Jason Zhu. 2022. “Forest through the trees: Building cross-sections of stock returns.” Working Paper. http://dx.doi.org/10.2139/ssrn.3493458.

Chen, Luyang, Markus Pelger, and Jason Zhu. 2023. “Deep learning in asset pricing.” Management Science. https://doi.org/10.48550/arXiv.1904.00745.

Coqueret, Guillaume, and Tony Guida. 2020. Machine learning for factor investing: R version. Chapman; Hall/CRC. https://www.mlfactor.com/.

Gu, Shihao, Bryan Kelly, and Dacheng Xiu. 2020. “Empirical asset pricing via machine learning.” Edited by Andrew Karolyi. Review of Financial Studies 33 (5): 2223–73. https://doi.org/10.1093/rfs/hhaa009.

Hornik, Kurt. 1991. “Approximation capabilities of multilayer feedforward networks.” Neural Networks 4 (2): 251–57. https://doi.org/10.1016/0893-6080(91)90009-T.

Hull, John C. 2020. Machine learning in business. An introduction to the world of data science. Independently published.

Jensen, Theis Ingerslev, Bryan T. Kelly, Semyon Malamud, and Lasse Heje Pedersen. 2022. “Machine Learning and the Implementable Efficient Frontier.” Working Paper. https://doi.org/10.2139/ssrn.3491942.

Jiang, Jingwen, Bryan T. Kelly, and Dacheng Xiu. 2023. “(Re-)Imag(in)ing Price Trends.” The Journal of Finance 78 (6): 3193–3249. https://doi.org/10.1111/jofi.13268.